介紹如何在 R 中使用 FactoMineR 套件進行主成分與階層式集群分析 HCPC 分析。
群集分析(clustering)是一種在多變量分析中很重要的資料探勘方法,其目的在於依據資料相似度找出適當的分群方式,常見的群集分析有階層式分群(hierarchical clustering)與分割式分群(partitioning clustering,例如 k-means)兩種。
HCPC(Hierarchical Clustering on Principal Components)是將多變量分析上的三種分析方法結合起來使用:
- 各種主成分分析法(PCA、CA、MCA、FAMD、MFA)。
- 階層式分群。
- 分割式分群。
以下將介紹為什麼要結合主成分與分群分析方法,並以 R 實作分析流程。
為什麼需要使用 HCPC?
連續型變數
當資料的維度很高(變數很多)、且資料類型屬於連續型變數時,主成分分析(PCA)可以降低資料的維度、保留重要的特徵,接著再以群集分析對主成分分析的結果進行分群。
我們可將主成分分析視為一種去除雜訊的步驟,讓群集分析的結果更加穩定,這個方法在資料維度較高的時候非常有用,例如基因表現資料。
類別型變數
若需要對類別型變數的資料進行群集分析,可先以對應分析(correspondence analysis,簡稱 CA,針對列聯表)與多重對應分析(multiple correspondence analysis,MCA,針對多維度類別型變數)將資料轉換成連續型變數(主成分),後續再以群集分析接著處理。
在這種狀況下,CA 或 MCA 可被視為一種將類別型變數轉換為連續型變數的資料前處理。
混合型變數
資料同時包含連續型與類別型兩種變數時,可以使用 FAMD(factor analysis of mixed data)或 MFA(multiple factor analysis)方法,後續再以群集分析接著處理。
R FactoMineR 套件
在 R 的 FactoMineR 套件中實作了 HCPC 分析方法,其分析流程如下:
- 各類主成分分析:包含 PCA、CA、MCA、MFA(依據資料類型與資料集結構選擇對應方法),在這個分析步驟中,可以選擇要保留多少主成分(預設值為
5)。 - 階層式分群:使用選定的各個主成分,根據華德法(Ward’s method)進行階層式分群。選用華德法的原因在於華德法與主成分分析的計算依據相同,都是資料的變異數(variance)。
- 根據階層樹選定群集個數,建立起始的資料分群。
- 分割式分群:以階層式分群結果為初始值,進行 k-means 分群。
這裡我們除了使用 FactoMineR 套件進行 HCPC 分析之外,還需要使用到 factoextra 套件來呈現視覺化的結果。首先安裝並載入這兩個必要套件:
# 安裝必要 R 套件 install.packages(c("FactoMineR", "factoextra")) # 載入必要 R 套件 library(factoextra) library(FactoMineR)
在FactoMineR 套件中最主要的分析工具就是 HCPC 這個函數,他可以接受各類主成分分析的結果,進行階層式分群,此函數的基本用法如下:
# HCPC 函數用法 HCPC(res, nb.clust = 0, min = 3, max = NULL, graph = TRUE)
res:各類主成分分析結果,可為 CA 分析的結果或data.frame。nb.clust:指定分群的群集個數,若為0則代表由使用者動態指定,若為-1則代表自動判斷最適合的分群。min與max:群集個數的下限與上限。graph:是否要以圖形顯示結果。
連續型變數實際範例
這裡我們以 USArrests 這個資料集為例,其資料結構如下:
# 查看資料結構 str(USArrests)
'data.frame': 50 obs. of 4 variables: $ Murder : num 13.2 10 8.1 8.8 9 7.9 3.3 5.9 15.4 17.4 ... $ Assault : int 236 263 294 190 276 204 110 238 335 211 ... $ UrbanPop: int 58 48 80 50 91 78 77 72 80 60 ... $ Rape : num 21.2 44.5 31 19.5 40.6 38.7 11.1 15.8 31.9 25.8 ...
先以 PCA 函數對連續型資料進行主成分分析:
# 主成分分析 res.pca <- PCA(USArrests, ncp = 3, graph = FALSE)
這裡我們保留前三個主成分(ncp = 3),並且不顯示圖形(graph = FALSE)。
若需要查看 PCA 所繪製的圖形,可以執行:
# 繪製主成分分析相關圖形 plot(res.pca, choix = "ind") plot(res.pca, choix = "var") plot(res.pca, choix = "varcor") # 當 scale.unit=FALSE 時使用
接著進行 HCPC 分析:
# HCPC 分析 res.hcpc <- HCPC(res.pca, graph = FALSE)
使用 factoextra 套件的 fviz_dend 繪製由階層式分群所產生的樹狀圖:
# 樹狀圖 fviz_dend(res.hcpc, cex = 0.7, # 文字大小 palette = "jco", # 文字配色(可參考 ?ggpubr::ggpar) rect = TRUE, rect_fill = TRUE, # 加入分群標示方框 rect_border = "jco", # 方框配色 labels_track_height = 0.8) # 文字顯示空間

這裡它將資料分為四群,從樹狀圖看起來四群的結構很漂亮,各群之間都有一定的距離。
我們也可以用 fviz_cluster 函數將每筆資料畫在主成分的座標圖形中,並以顏色標示分群,觀察群聚的情況:
# 群聚圖 fviz_cluster(res.hcpc, repel = TRUE, # 避免文字重疊 show.clust.cent = TRUE, # 顯示各群中心點 palette = "jco") # 文字配色(可參考 ?ggpubr::ggpar)
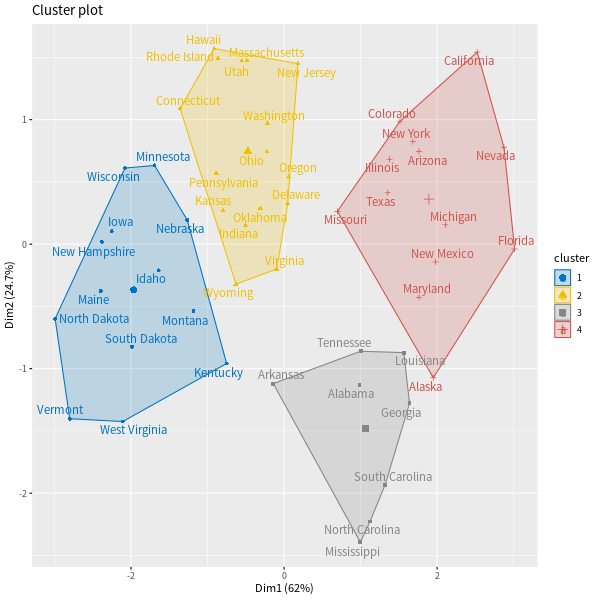
亦可將樹狀圖與群聚圖合併成一張 3D 的圖形:
# 樹狀圖與群聚圖合併 plot(res.hcpc, choice = "3D.map")
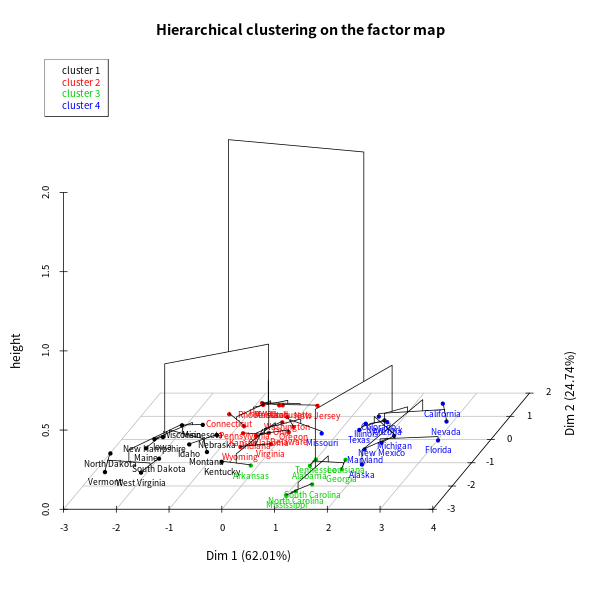
在 HCPC 的分析結果(res.hcpc)中,還包含了許多資訊:
data.clust:原始資料外加一欄分群資訊。desc.var:變數相關的分群資訊。desc.ind:個體相關的分群資訊。desc.axes:主成分座標軸相關的分群資訊。
原始資料加上分群結果可由 data.clust 取得:
# 原始資料加上分群結 head(res.hcpc$data.clust)
Murder Assault UrbanPop Rape clust Alabama 13.2 236 58 21.2 3 Alaska 10.0 263 48 44.5 4 Arizona 8.1 294 80 31.0 4 Arkansas 8.8 190 50 19.5 3 California 9.0 276 91 40.6 4 Colorado 7.9 204 78 38.7 4
檢視變數相關的分群資訊(呼叫 catdes 函數分析的結果):
# 變數相關的分群資訊 res.hcpc$desc.var$quanti
$`1`
v.test Mean in category Overall mean sd in category Overall sd
UrbanPop -3.898420 52.07692 65.540 9.691087 14.329285
Murder -4.030171 3.60000 7.788 2.269870 4.311735
Rape -4.052061 12.17692 21.232 3.130779 9.272248
Assault -4.638172 78.53846 170.760 24.700095 82.500075
p.value
UrbanPop 9.682222e-05
Murder 5.573624e-05
Rape 5.076842e-05
Assault 3.515038e-06
$`2`
v.test Mean in category Overall mean sd in category Overall sd
UrbanPop 2.793185 73.87500 65.540 8.652131 14.329285
Murder -2.374121 5.65625 7.788 1.594902 4.311735
p.value
UrbanPop 0.005219187
Murder 0.017590794
$`3`
v.test Mean in category Overall mean sd in category Overall sd
Murder 4.357187 13.9375 7.788 2.433587 4.311735
Assault 2.698255 243.6250 170.760 46.540137 82.500075
UrbanPop -2.513667 53.7500 65.540 7.529110 14.329285
p.value
Murder 1.317449e-05
Assault 6.970399e-03
UrbanPop 1.194833e-02
$`4`
v.test Mean in category Overall mean sd in category Overall sd
Rape 5.352124 33.19231 21.232 6.996643 9.272248
Assault 4.356682 257.38462 170.760 41.850537 82.500075
UrbanPop 3.028838 76.00000 65.540 10.347798 14.329285
Murder 2.913295 10.81538 7.788 2.001863 4.311735
p.value
Rape 8.692769e-08
Assault 1.320491e-05
UrbanPop 2.454964e-03
Murder 3.576369e-03
檢視主成分座標軸相關的分群資訊(呼叫 catdes 函數分析的結果):
# 主成分座標軸相關的分群資訊 res.hcpc$desc.axes$quanti
$`1`
v.test Mean in category Overall mean sd in category Overall sd
Dim.1 -5.175764 -1.964502 -5.639933e-16 0.6192556 1.574878
p.value
Dim.1 2.269806e-07
$`2`
v.test Mean in category Overall mean sd in category Overall sd
Dim.2 3.585635 0.7428712 -5.369316e-16 0.6137936 0.9948694
p.value
Dim.2 0.0003362596
$`3`
v.test Mean in category Overall mean sd in category Overall sd
Dim.1 2.058338 1.0610731 -5.639933e-16 0.5146613 1.5748783
Dim.3 2.028887 0.3965588 3.535366e-17 0.3714503 0.5971291
Dim.2 -4.536594 -1.4773302 -5.369316e-16 0.5750284 0.9948694
p.value
Dim.1 3.955769e-02
Dim.3 4.246985e-02
Dim.2 5.717010e-06
$`4`
v.test Mean in category Overall mean sd in category Overall sd
Dim.1 4.986474 1.892656 -5.639933e-16 0.6126035 1.574878
p.value
Dim.1 6.149115e-07
檢視個體相關的分群資訊(para 是最接近群聚中心的幾個個體,dist 是最遠離群聚中心的幾個個體):
# 最接近群聚中心的幾個個體 res.hcpc$desc.ind$para
Cluster: 1
Idaho South Dakota Maine Iowa New Hampshire
0.3674381 0.4993032 0.5012072 0.5533105 0.5891145
------------------------------------------------------------
Cluster: 2
Ohio Oklahoma Pennsylvania Kansas Indiana
0.2796100 0.5047549 0.5088363 0.6039091 0.7100820
------------------------------------------------------------
Cluster: 3
Alabama South Carolina Georgia Tennessee Louisiana
0.3553460 0.5335189 0.6136865 0.8522640 0.8780872
------------------------------------------------------------
Cluster: 4
Michigan Arizona New Mexico Maryland Texas
0.3246254 0.4532480 0.5176322 0.9013514 0.9239792
# 最遠離群聚中心的幾個個體 res.hcpc$desc.ind$dist
Cluster: 1
Vermont North Dakota West Virginia South Dakota Maine
3.322204 2.892724 2.729278 2.248533 2.228610
------------------------------------------------------------
Cluster: 2
Rhode Island Massachusetts Utah New Jersey Washington
2.663499 2.492513 2.321858 2.270583 2.225956
------------------------------------------------------------
Cluster: 3
Mississippi North Carolina South Carolina Arkansas Alabama
3.065029 2.925245 2.430529 1.912159 1.884601
------------------------------------------------------------
Cluster: 4
Nevada California Alaska Florida Colorado
3.285915 3.193428 2.624992 2.431217 2.364583
類別型變數實際範例
這裡我們以 FactoMineR 套件中所附帶的 tea 資料集來示範類別型的資料分析流程。
# 載入 tea 資料集 data(tea) # 查看資料結構 str(tea)
'data.frame': 300 obs. of 36 variables: $ breakfast : Factor w/ 2 levels "breakfast","Not.breakfast": 1 1 2 2 1 2 1 2 1 1 ... $ tea.time : Factor w/ 2 levels "Not.tea time",..: 1 1 2 1 1 1 2 2 2 1 ... $ evening : Factor w/ 2 levels "evening","Not.evening": 2 2 1 2 1 2 2 1 2 1 ... $ lunch : Factor w/ 2 levels "lunch","Not.lunch": 2 2 2 2 2 2 2 2 2 2 ... $ dinner : Factor w/ 2 levels "dinner","Not.dinner": 2 2 1 1 2 1 2 2 2 2 ... $ always : Factor w/ 2 levels "always","Not.always": 2 2 2 2 1 2 2 2 2 2 ... $ home : Factor w/ 2 levels "home","Not.home": 1 1 1 1 1 1 1 1 1 1 ... $ work : Factor w/ 2 levels "Not.work","work": 1 1 2 1 1 1 1 1 1 1 ... $ tearoom : Factor w/ 2 levels "Not.tearoom",..: 1 1 1 1 1 1 1 1 1 2 ... $ friends : Factor w/ 2 levels "friends","Not.friends": 2 2 1 2 2 2 1 2 2 2 ... $ resto : Factor w/ 2 levels "Not.resto","resto": 1 1 2 1 1 1 1 1 1 1 ... $ pub : Factor w/ 2 levels "Not.pub","pub": 1 1 1 1 1 1 1 1 1 1 ... $ Tea : Factor w/ 3 levels "black","Earl Grey",..: 1 1 2 2 2 2 2 1 2 1 ... $ How : Factor w/ 4 levels "alone","lemon",..: 1 3 1 1 1 1 1 3 3 1 ... $ sugar : Factor w/ 2 levels "No.sugar","sugar": 2 1 1 2 1 1 1 1 1 1 ... $ how : Factor w/ 3 levels "tea bag","tea bag+unpackaged",..: 1 1 1 1 1 1 1 1 2 2 ... $ where : Factor w/ 3 levels "chain store",..: 1 1 1 1 1 1 1 1 2 2 ... $ price : Factor w/ 6 levels "p_branded","p_cheap",..: 4 6 6 6 6 3 6 6 5 5 ... $ age : int 39 45 47 23 48 21 37 36 40 37 ... $ sex : Factor w/ 2 levels "F","M": 2 1 1 2 2 2 2 1 2 2 ... $ SPC : Factor w/ 7 levels "employee","middle",..: 2 2 4 6 1 6 5 2 5 5 ... $ Sport : Factor w/ 2 levels "Not.sportsman",..: 2 2 2 1 2 2 2 2 2 1 ... $ age_Q : Factor w/ 5 levels "15-24","25-34",..: 3 4 4 1 4 1 3 3 3 3 ... $ frequency : Factor w/ 4 levels "1/day","1 to 2/week",..: 1 1 3 1 3 1 4 2 3 3 ... $ escape.exoticism: Factor w/ 2 levels "escape-exoticism",..: 2 1 2 1 1 2 2 2 2 2 ... $ spirituality : Factor w/ 2 levels "Not.spirituality",..: 1 1 1 2 2 1 1 1 1 1 ... $ healthy : Factor w/ 2 levels "healthy","Not.healthy": 1 1 1 1 2 1 1 1 2 1 ... $ diuretic : Factor w/ 2 levels "diuretic","Not.diuretic": 2 1 1 2 1 2 2 2 2 1 ... $ friendliness : Factor w/ 2 levels "friendliness",..: 2 2 1 2 1 2 2 1 2 1 ... $ iron.absorption : Factor w/ 2 levels "iron absorption",..: 2 2 2 2 2 2 2 2 2 2 ... $ feminine : Factor w/ 2 levels "feminine","Not.feminine": 2 2 2 2 2 2 2 1 2 2 ... $ sophisticated : Factor w/ 2 levels "Not.sophisticated",..: 1 1 1 2 1 1 1 2 2 1 ... $ slimming : Factor w/ 2 levels "No.slimming",..: 1 1 1 1 1 1 1 1 1 1 ... $ exciting : Factor w/ 2 levels "exciting","No.exciting": 2 1 2 2 2 2 2 2 2 2 ... $ relaxing : Factor w/ 2 levels "No.relaxing",..: 1 1 2 2 2 2 2 2 2 2 ... $ effect.on.health: Factor w/ 2 levels "effect on health",..: 2 2 2 2 2 2 2 2 2 2 ...
首先以 MCA 進行處理,並保留 MCA 的前 20 維度:
# MCA 分析 res.mca <- MCA(tea, ncp = 20, # 保留前 20 維度 quanti.sup = 19, # 連續型補充變數 quali.sup = c(20:36), # 類別型補充變數 graph = FALSE)
res.mca 之中有許多 MCA 的分析結果資訊,例如查看各維度的變異數比重:
# 查看各維度的變異數比例 res.mca$eig
eigenvalue percentage of variance cumulative percentage of variance dim 1 0.14827441 9.884961 9.884961 dim 2 0.12154673 8.103115 17.988076 dim 3 0.09000954 6.000636 23.988712 dim 4 0.07805440 5.203627 29.192339 dim 5 0.07374870 4.916580 34.108919 dim 6 0.07138044 4.758696 38.867615 dim 7 0.06782906 4.521937 43.389552 dim 8 0.06532655 4.355103 47.744656 dim 9 0.06184167 4.122778 51.867433 dim 10 0.05852817 3.901878 55.769311 dim 11 0.05707772 3.805181 59.574493 dim 12 0.05441920 3.627946 63.202439 dim 13 0.05192969 3.461979 66.664418 dim 14 0.04874462 3.249641 69.914060 dim 15 0.04831065 3.220710 73.134770 dim 16 0.04690465 3.126977 76.261747 dim 17 0.04554779 3.036519 79.298266 dim 18 0.04024922 2.683281 81.981547 dim 19 0.03812120 2.541414 84.522961 dim 20 0.03657138 2.438092 86.961053 dim 21 0.03566464 2.377643 89.338696 dim 22 0.03484898 2.323266 91.661961 dim 23 0.03082882 2.055255 93.717216 dim 24 0.02873151 1.915434 95.632650 dim 25 0.02732068 1.821378 97.454028 dim 26 0.02110048 1.406699 98.860727 dim 27 0.01708910 1.139273 100.000000
接著進行 HCPC 分析:
# HCPC 分析 res.hcpc <- HCPC (res.mca, graph = FALSE, max = 3)
繪製樹狀圖:
# 樹狀圖 fviz_dend(res.hcpc, show_labels = FALSE, palette = "jco")
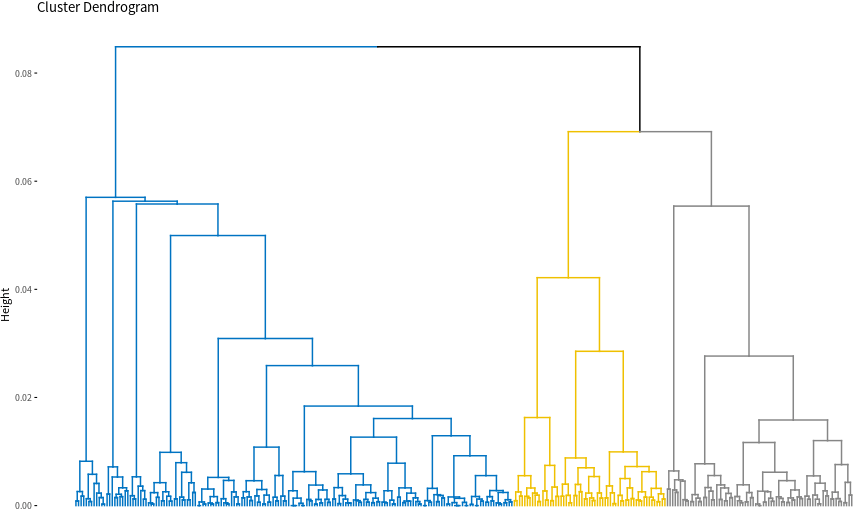
繪製群聚圖:
# 群聚圖 fviz_cluster(res.hcpc, geom = "point", palette = "jco")
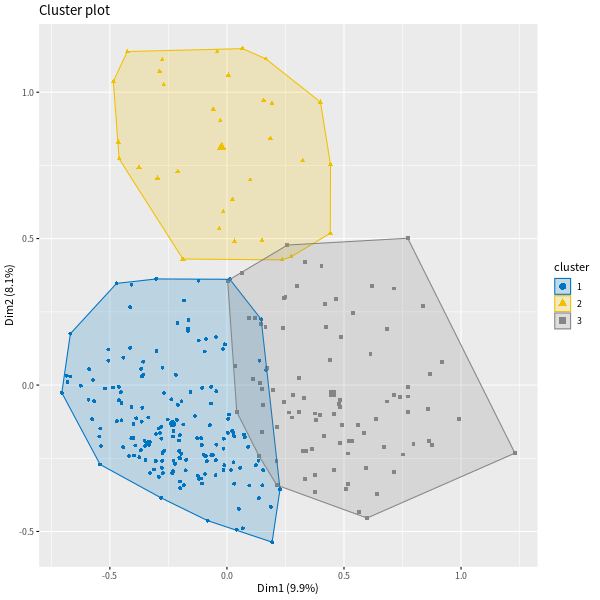
這裡一樣可以從 HCPC 分析的結果中取得各種分群的細部資訊:
# 原始資料加上分群結 head(res.hcpc$data.clust) # 變數相關的分群資訊 res.hcpc$desc.var$category res.hcpc$desc.var$test.chi2 # 主成分座標軸相關的分群資訊 res.hcpc$desc.axes$quanti res.hcpc$desc.axes$quanti.var # 最接近群聚中心的幾個個體 res.hcpc$desc.ind$para # 最遠離群聚中心的幾個個體 res.hcpc$desc.ind$dist
參考資料:STHDA、HCPC、FactoMineR、RPubs、群集分析

