介紹如何使用 Excel 檢測離群值（outlier）或極端值（extreme value），找出可能有問題的資料。
通常若想要檢查資料之中是否存在離群值或極端值，首先會先對資料進行常態性檢定，確認資料來自於常態分布之後，再計算第一四分位數（Q1）、第三四分位數（Q3）與四分位距（IQR），若資料超出
Q1 - 1.5 * IQR 到 Q3 + 1.5 * IQR 這個範圍，就有可能是有問題的資料。
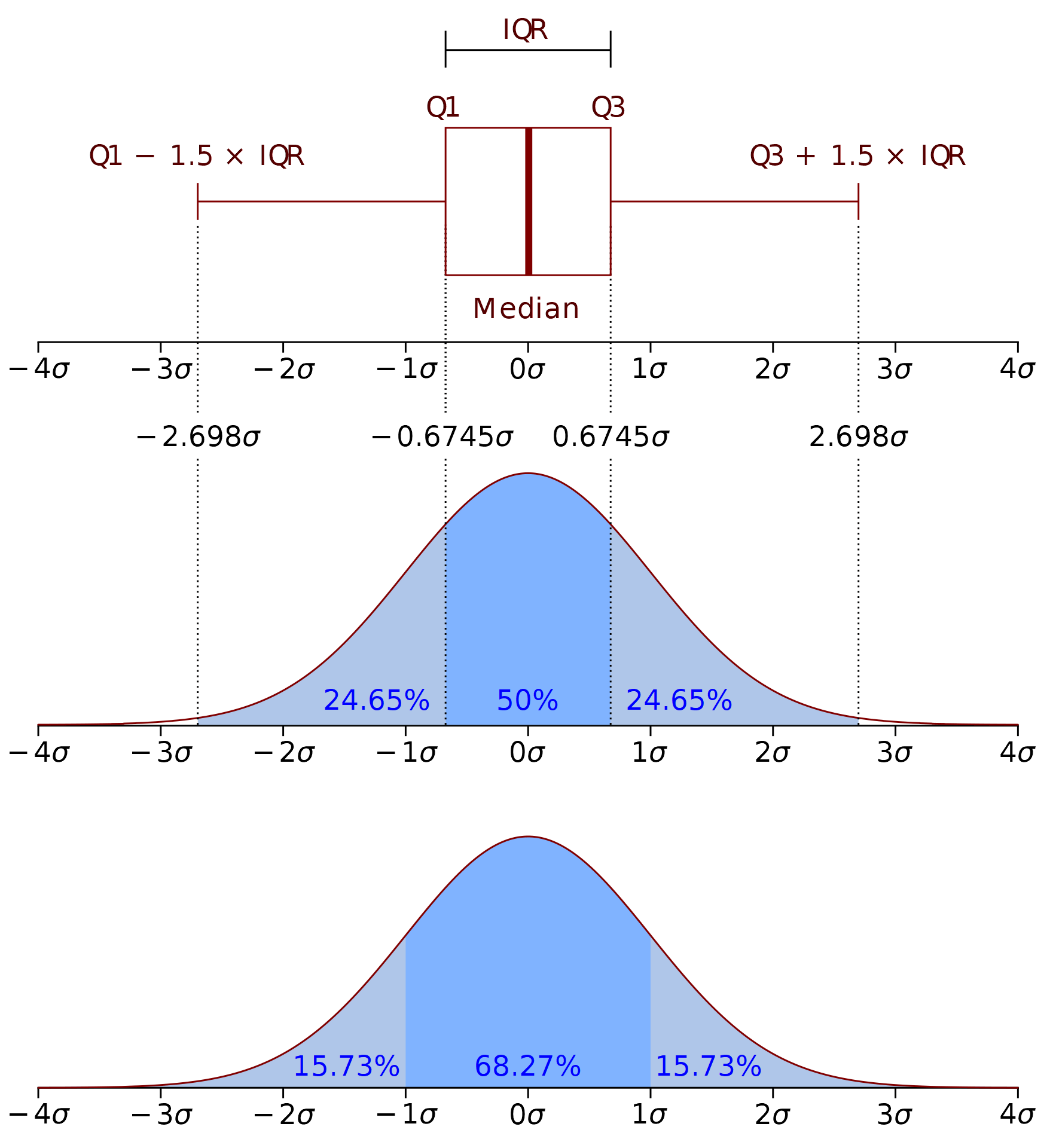
關於四分位距與離群值的解釋，可參考維基百科的說明。
由於 Excel 並沒有提供常態性檢定的工具，建議可以改用 R 等統計工具進行常態性檢定。
計算四分位數（Q1 與 Q3）
假設我們有一些數值資料如下：
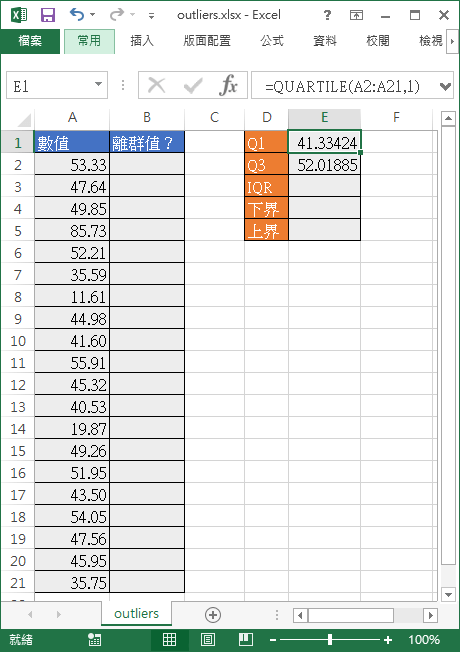
在檢測離群值之前，首先要使用 QUARTILE 計算 Q1 與 Q3 的值，QUARTILE 的第一個參數就是放原始的資料範圍，而第二個參數若填入 1 則代表計算 Q1，若填入 3 則代表計算 Q3：
=QUARTILE(A2:A21,1) =QUARTILE(A2:A21,3)
計算的結果如下：
四分位距（IQR）
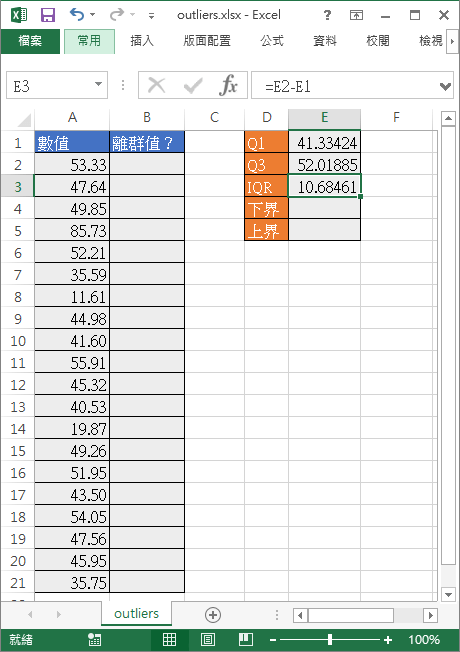
接著將 Q3 的值減掉 Q1 的值，就可以算出 IQR：
=E2-E1
判斷離群值
依照上面介紹的公式，算出正常值的上下界：
=E1-1.5*E3 =E2+1.5*E3
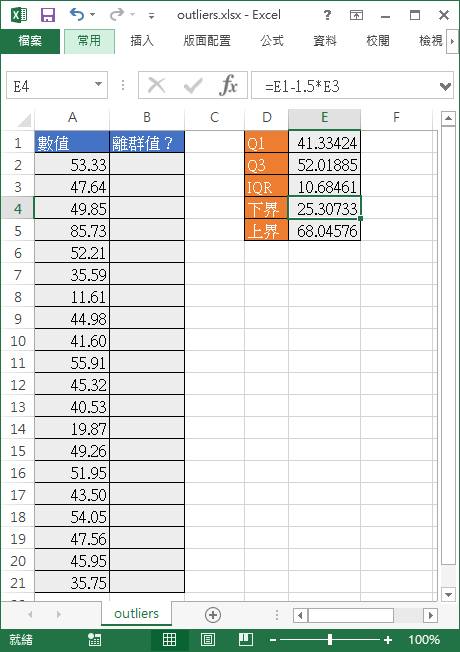
這裡算出來的上下界分別是 25.3 與 68.0 左右，原則上來說，資料只要超出這個範圍，就非常有可能是有問題的。
最後使用 OR 函數，檢查每一筆原始資料是否有超出上界或下界，如果超出去的話就判定為離群值。
=OR(A2<$E$4,A2>$E$5)
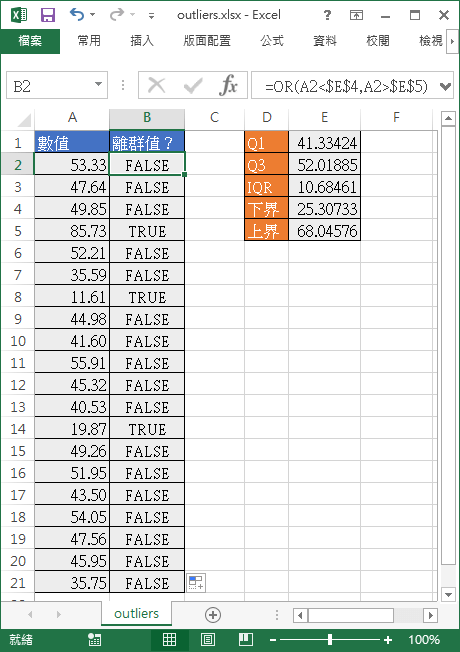
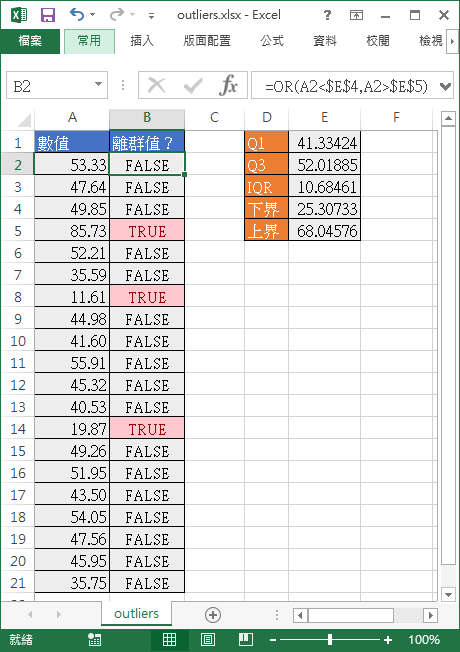
如果感覺單純的文字標示不夠明顯的話，可以使用條件格式化儲存格的方式，將判定為離群值（TRUE）的儲存格塗上顏色。
參考資料：How-To Geek、AbsentData
發佈留言