介紹如何使用 R 語言進行基本的存活分析,繪製存活曲線,以 log-rank 檢定判定存活曲線是否有差異。
在許多的癌症研究中,都會對存活時間(survival time)進行評估,存活時間只是一種統稱,其本質上的意義是從觀測開始到發生特定事件的時間,除了用於病患在接受治療後到死亡的時間之外,也可以用於治療後到疾病復發的時間,在進行研究時必須先明確定義事件類型,以及量測時間的起訖點。
若在研究的期間,我們可以觀測到每位病患的事件(復發或死亡等)發生時間點,則可以使用許多不同的統計分析方法,但在實務上常會遇到當研究終止時,卻還有一些病患尚未發生特定事件,因此這些事件的實際發生時間點在研究上是無法觀測到的,另外存活時間的資料通常不會符合常態分佈(normal distribution),而是大部分事件發生在早期,晚期事件通常較少,像這樣特性的資料就適合用存活分析的方式來處理。
設限資料
在存活分析中,通常只能觀測到部分受試者的事件發生,也就是說有一些受試者的事件發生點是未知的,這種現象稱為設限(censoring),而造成設限的原因可能會有以下幾種:
- 研究計畫結束時,受試者還是沒有發生事件(復發或死亡)。
- 受試者中途失去聯繫(例如轉院),無法進行後續追蹤。
- 受試者因為某些原因退出研究(例如藥物不良反應等)。
以上幾種設限資料都會低估實際的存活時間,也就是說當我們把存活時間畫在水平數線上的時候,實際的的事件發生點是位於追蹤區間的右方(但實際發生點是未知的),像這樣的狀況稱為右設限(right censoring)。
資料設限的狀況也可能發生在左方,舉例來說,假設我們要研究病患經過外科手術移除腫瘤之後到癌症復發的時間,若病患在完成手術後三個月才開始觀測是否復發,則在第三個月所觀測到的復發事件就屬於左設限(left censoring)的資料,因為其實際復發的時間點是小於三個月的。
觀測資料也有可能出現區間設限(interval censoring)的狀況,也就是說受試者在中途暫時離開,然後過了一段時間又回來,如果再度回來的時候,發生了特定事件,我們就無法確定這個事件是在他離開期間的哪一個時間點發生的。
一般來說遇到設限的資料時,就會需要特別的分析方法來處理,而右設限的資料是最常見的,以下我們將介紹右設限資料的存活分析方法。
存活函數與風險函數
存活分析的模型通常會以存活函數(survival function)與風險函數(hazard function)來表示。存活函數 \(S(t)\) 代表受試者從觀測時間起始點存活至時間 \(t\) 的機率,這個存活函數描述了受試者的整個存活歷程,提供了存活分析中非常關鍵的資訊。
\[S(t) = P(T>t)\]
風險函數通常以 \(h(t)\) 或 \(\lambda(t)\) 來表示,其意義為受試者在時間 \(t\) 發生事件的風險,換句話說就是受試者存活至時間 \(t\) 時發生事件的風險。
\[h(t) = \lim_{\delta\rightarrow{0}}\frac{P(t < {T} < t+\delta|T > {t})}{\delta}\]
累積風險(cumulative hazard)的定義則為
\[H(t) = \int_0^th(t)\,dt = -\log(S(t))\]
Kaplan-Meier 方法
Kaplan-Meier 方法是一種無母數的存活函數估計方法,不管資料是否有設限皆可使用,假設現在我們有 \(k\) 個受試者,其事件發生的時間點為 \(t_1 < t_2 < t_3 < \dots < t_k\),而這些事件的發生都是獨立的,則存活函數位於 \(t_j\) 時間點的存活函數值 \(S(t_j)\) 可以使用以下公式來估計:
\[S(t_j) = S(t_{j-1})\big(1-\frac{d_j}{n_j}\big)\]
其中
- \(S(t_{j-1})\) 是時間 \(t_{j-1}\) 的存活函數值。
- \(n_j\) 為在 \(t_j\) 時間點之前的那個時間點,還存活的受試者數量。
- \(d_j\) 為在 \(t_j\) 時間點的事件數量。
- \(t_0\) 為 \(0\)。
- \(S(0)\) 為 \(1\)。
R 存活分析套件
安裝並載入 survival 與 survminer 套件:
# 安裝 survival 與 survminer 套件 install.packages(c("survival", "survminer")) # 載入 survival 與 survminer 套件 library("survival") library("survminer")
在 survival 套件中有一個 lung 資料集,裡面有一些肺癌病患的資料,以 head 查看一下其中的內容:
# 查看 lung 資料集內容 head(lung)
inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss 1 3 306 2 74 1 1 90 100 1175 NA 2 3 455 2 68 1 0 90 90 1225 15 3 3 1010 1 56 1 0 90 90 NA 15 4 5 210 2 57 1 1 90 60 1150 11 5 1 883 2 60 1 0 100 90 NA 0 6 12 1022 1 74 1 1 50 80 513 0
以下是 lung 資料集的各資料欄位意義:
| 欄位 | 意義 |
|---|---|
inst |
機構代碼。 |
time |
存活時間,單位為天。 |
status |
設限狀態,1 代表設限,2 代表死亡。 |
age |
年齡,單位為年。 |
sex |
性別,1 代表男性,2 代表女性。 |
ph.ecog |
醫師判定的 ECOG 表現分數,0 代表無症狀,1 代表有症狀但完全不臥床,2 代表不到 50% 的時間臥床,3 代表 50% 以上的時間臥床,4 代表整天臥床。 |
ph.karno |
醫師判定的 Karnofsky 表現分數,0 分代表最差,100 分代表最好。 |
pat.karno |
病患自己判定的 Karnofsky 表現分數,0 分代表最差,100 分代表最好。 |
meal.cal |
進餐消耗的卡路里。 |
wt.loss |
最近六個月的體重減輕,單位為磅。 |
計算存活函數
survival 套件所提供的 survfit() 可以透過 Kaplan-Meier 演算法計算存活函數估計值,使用時要搭配 Surv() 函數建立存活物件,並以一個公式(formula)指定分析的模型:
# 以 Kaplan-Meier 計算存活函數 fit <- survfit(Surv(time, status) ~ sex, data = lung)
這裡所使用的公式為 Surv(time, status) ~ sex,公式左側一定是一個 Surv 物件,而右側則是用於分組的變數,以這個公式來說就是根據不同性別來計算存活函數。
若要檢視存活函數簡略資訊,可以使用 print() 輸出 survfit 物件:
# 檢視存活函數簡略資訊 print(fit)
Call: survfit(formula = Surv(time, status) ~ sex, data = lung)
n events median 0.95LCL 0.95UCL
sex=1 138 112 270 212 310
sex=2 90 53 426 348 550
以 print() 函數輸出 survfit 物件時,預設會顯示存活函數的基本資訊,包含:
n:受試者的數量。events:事件的數量。median:中位存活時間(median survival time),男性與女性的中位存活時間分別為270與426。。0.95LCL與0.95UCL:中位存活時間的 95% 信賴區間。
若要更詳盡的存活函數資訊,可以使用 summary() 來輸出 survfit 物件:
# 檢視存活函數詳細資訊 summary(fit)
Call: survfit(formula = Surv(time, status) ~ sex, data = lung)
sex=1
time n.risk n.event survival std.err lower 95% CI upper 95% CI
11 138 3 0.9783 0.0124 0.9542 1.000
12 135 1 0.9710 0.0143 0.9434 0.999
13 134 2 0.9565 0.0174 0.9231 0.991
15 132 1 0.9493 0.0187 0.9134 0.987
26 131 1 0.9420 0.0199 0.9038 0.982
[略]
另外存活函數簡略資訊的表格資料,可以從 summary() 的 table 或其他元素取得:
# 取得存活函數簡略資訊表格資料 summary(fit)$table
records n.max n.start events rmean se(rmean) median 0.95LCL 0.95UCL sex=1 138 138 138 112 326.0841 22.91156 270 212 310 sex=2 90 90 90 53 460.6473 34.68985 426 348 550
surv_summary() 函數也可以用來取得整理好的存活函數表格資料:
# 存活函數詳細資訊 surv_summary(fit)
time n.risk n.event n.censor surv std.err upper lower strata sex 1 11 138 3 0 0.97826087 0.01268978 1.0000000 0.95423012 sex=1 1 2 12 135 1 0 0.97101449 0.01470747 0.9994124 0.94342350 sex=1 1 3 13 134 2 0 0.95652174 0.01814885 0.9911586 0.92309525 sex=1 1 4 15 132 1 0 0.94927536 0.01967768 0.9866017 0.91336116 sex=1 1 5 26 131 1 0 0.94202899 0.02111708 0.9818365 0.90383547 sex=1 1 [略]
繪製存活函數圖形
若要繪製存活函數的圖形,可以使用 survminer 套件所提供的 ggsurvplot() 函數:
# 繪製存活函數圖形 ggsurvplot(fit)
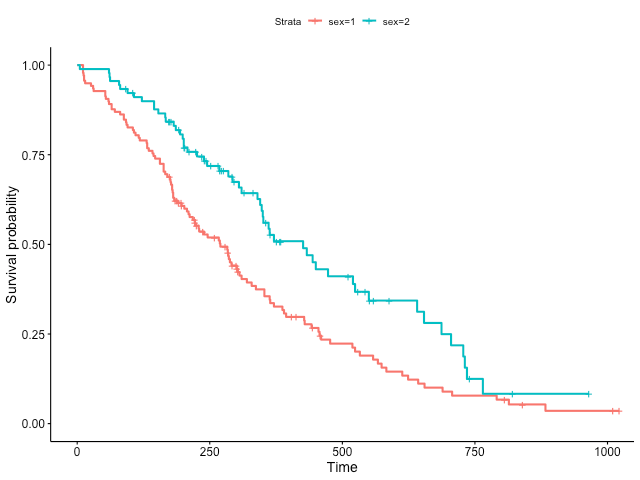
在圖形中的兩條不同顏色的存活曲線,分別代表不同群體(男性與女性)的存活函數,X 軸代表的是時間,Y 軸代表存活機率或是存活的人數比例,當曲線下降時代表該處有事件發生,而曲線上的垂直標記點則代表該處有受試者發生設限。
在時間為零的那一點,存活函數的值是 1.0,代表所有人都處於存活的狀態,而在時間為 250 的時候,男性與女性的存活機率分別為 0.55 與 0.75 左右。
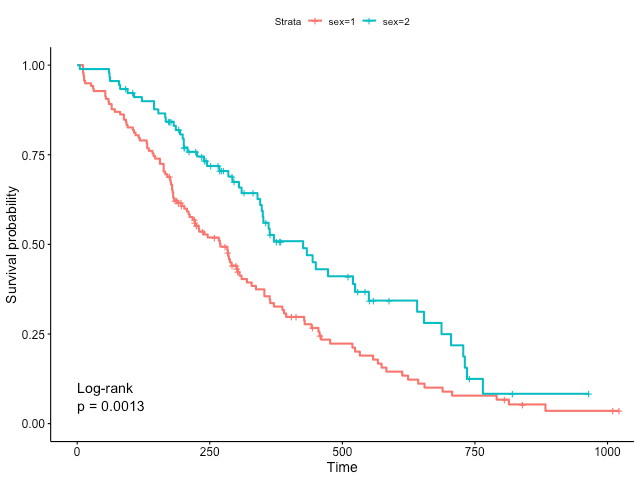
若要顯示檢定不同存活函數之間是否有差異的 p-value,可以將 pval 參數設定為 TRUE,並可搭配相關參數顯示檢定方法,以及文字的位置:
# 繪製存活函數圖形(顯示 p-value) ggsurvplot(fit, pval = TRUE, # 顯示 p-value pval.method = TRUE, # 顯示 p-value 計算方式 pval.coord = c(0, 0.05), # 指定 p-value 文字座標 pval.method.coord = c(0, 0.1)) # 指定 p-value 計算方式文字座標
若要繪製存活函數的信賴區間,可以將 conf.int 參數設定為 TRUE:
# 繪製存活函數圖形(顯示信賴區間) ggsurvplot(fit, conf.int = TRUE)
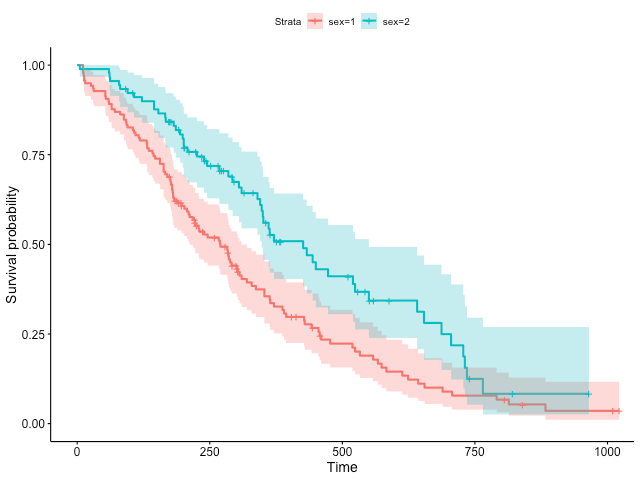
存活函數的信賴區間在尾端相對較寬,主要的因素在於實務上總是會有一些受試者中途失去聯繫、退出計畫,或是在研究計畫結束時,受試者還是沒有發生事件等,這些因素都會造成存活函數的信賴區間擴大。
ggsurvplot() 函數還有許多繪圖選項可以使用,例如顯示 risk table、標示中位數存活時間、更改配色等:
# 繪製存活函數圖形 ggsurvplot(fit, pval = TRUE, # 顯示 p-value conf.int = TRUE, # 顯示信賴區間 risk.table = TRUE, # 顯示 risk table risk.table.col = "strata", # 以群組指定 risk table 顏色 surv.median.line = "hv", # 標示中位數存活時間 ggtheme = theme_bw(), # 指定佈景主題 palette = c("#E7B800", "#2E9FDF")) # 指定色盤

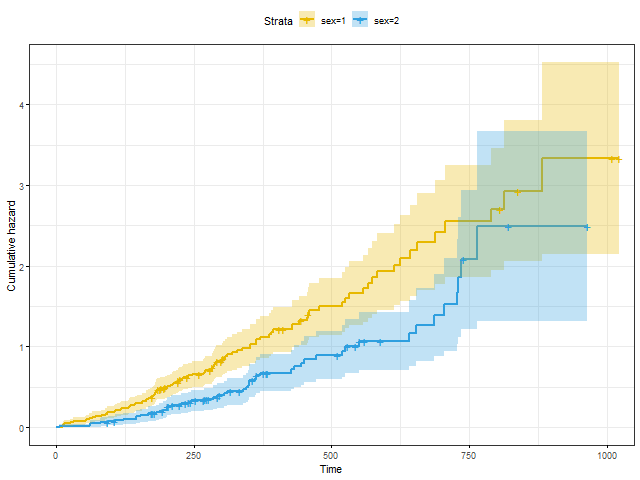
若要繪製累積風險函數,可以將 fun 參數設定為 cumhaz:
# 繪製累積風險函數圖形 ggsurvplot(fit, conf.int = TRUE, # 顯示信賴區間 risk.table.col = "strata", # 以群組指定 risk table 顏色 ggtheme = theme_bw(), # 指定佈景主題 palette = c("#E7B800", "#2E9FDF"), # 指定色盤 fun = "cumhaz") # 繪製累積風險函數
Log-Rank 檢定
Log-rank 檢定是最常用來判定兩條存活曲線是否存在差異的無母數方法,在 R 中我們可以使用 survdiff() 這個函數來進行 log-rank 檢定:
# 以 Log-Rank 檢定檢查多條存活函數是否有差異 surv_diff <- survdiff(Surv(time, status) ~ sex, data = lung) print(surv_diff)
Call:
survdiff(formula = Surv(time, status) ~ sex, data = lung)
N Observed Expected (O-E)^2/E (O-E)^2/V
sex=1 138 112 91.6 4.55 10.3
sex=2 90 53 73.4 5.68 10.3
Chisq= 10.3 on 1 degrees of freedom, p= 0.001
Log-rank 檢定的虛無假設(null hypothesis)是兩個群體的存活函數沒有存在差異,其採用的檢定統計量在虛無假設之下符合自由度爲 1 的卡方分佈(比較兩個群體時),在這份輸出報表中的 Chisq 就是統計量的數值,而 p 就是 p-value,以此例來說兩條存活曲線存在顯著差異。
參考資料
- STHDA:Survival Analysis Basics
- STHDA:Cox Proportional-Hazards Model
- STHDA:Cox Model Assumptions
- BIMS 8382:Survival Analysis with R
- Emily C. Zabor:Survival Analysis in R
- Yi-Ju Tseng:用 R 畫存活曲線 Survival curve
- Survival Analysis Part I: Basic concepts and first analyses
- R Views:Survival Analysis with R

