Excel 規劃求解：二元變數尋找最佳解教學與範例

介紹如何使用 Excel 的規劃求解功能，在二元變數的問題上尋找各種條件下的最佳解。

產品生產問題

假設某工廠使用三種原料依照不同比例製作成兩種產品，每單位產品所需要的原料與獲利如下：

	A 原料	B 原料	C 原料	獲利
每單位甲產品	5 公斤	3 公斤	3 公斤	600 元
每單位乙產品	3 公斤	6 公斤	3 公斤	700 元

如果今天工廠進了以下的原料：

• A 原料：1000 公斤。
• B 原料：1020 公斤。
• C 原料：660 公斤。

這時候甲、乙兩種產品各應生產多少單位才能獲得最大利潤？又此時利潤為多少？

假設甲產品生產了 x 單位，而乙產品生產了 y 單位。由於原料有限，所以會有以下的限制條件：

另外由於 x 與 y 都是產品生產量，所以值必須大於或等於 0。

在符合以上這些條件之下，我們希望總體的獲利可以達到最大值：

找最佳解

我們先將以上的資料與條件放入 Excel 表格中：

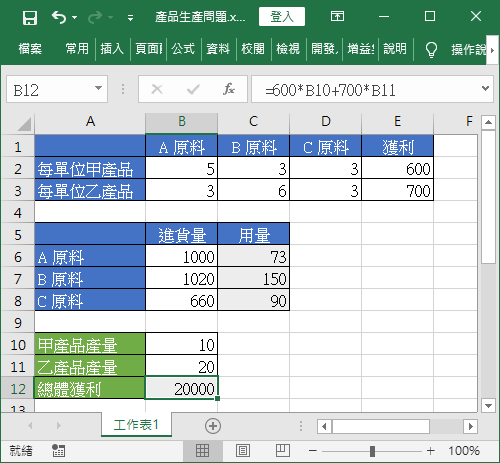
這裡的三種原料用量是根據甲、乙兩種產品的產量以公式計算的，例如 A 原料的用量公式就是：

=B2*B10+B3+B11

其餘以此類推，而總體利潤也是根據產品產量以公式自動計算：

=600*B10+700*B11

接著參考 Excel 啟用規劃求解增益集教學，啟用規劃求解功能，依照以下步驟使用規劃求解自動尋找最佳解。
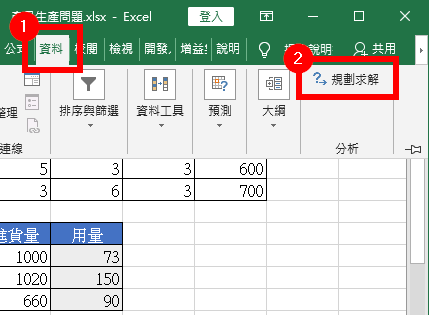
Step 1
在「資料」頁籤中選擇「規劃求解」。

Step 2
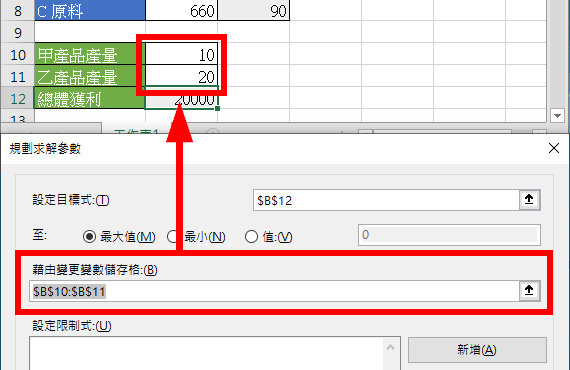
在這個問題中，我們會希望產生最大的總體獲利，所以將「目標式」設定為總體獲利的位置，最佳化的選項保持為「最大值」。

Step 3
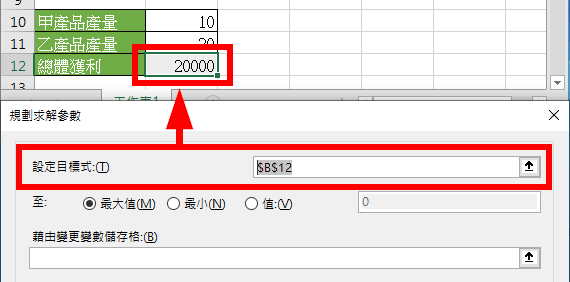
在這個問題中我們可以自由控制的變數就是甲、乙兩種產品的生產量，所以將「變更變數」設定為這兩種產品的生產量。

Step 4
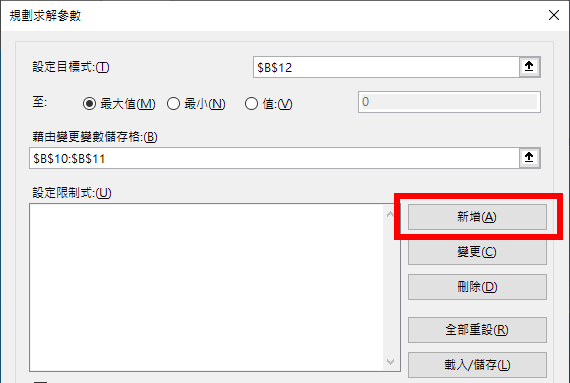
點選「新增」，加入限制條件。

Step 5
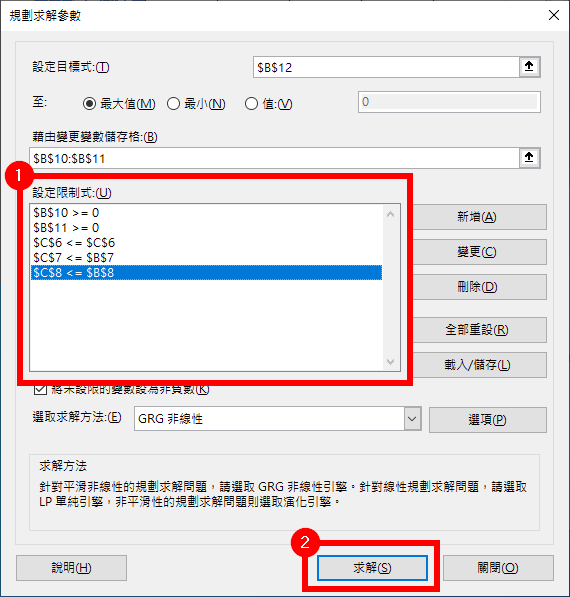
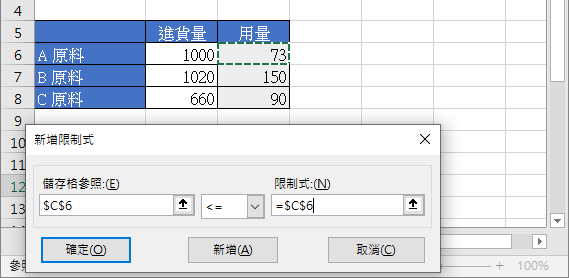
加入整理好的限制條件，也就是原料用量不可以超過原料的進貨量，以及產品的產量一定要大於或等於 0。

Step 6
加入所有限制條件之後，點選「求解」。

Step 7
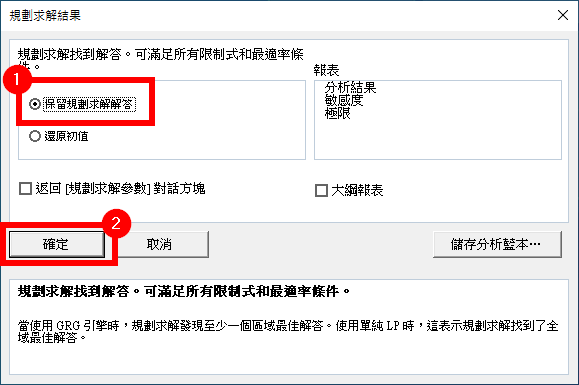
找到最佳解之後，選擇「保留規劃求解解答」，然後點選「確定」。

Step 8
這樣就找到最佳的生產方案了。

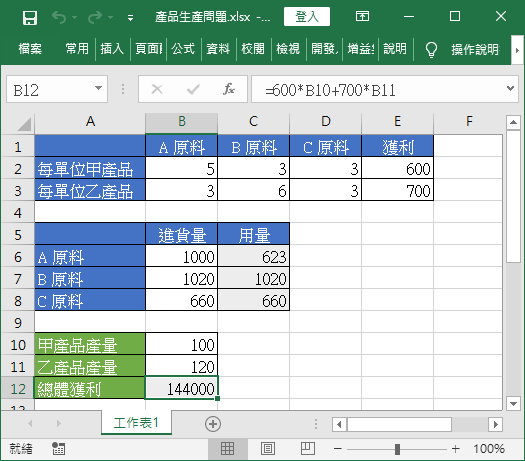
在這個最佳的方案中，甲產品生產 100 單位，乙產品生產 120 單位，產生的總體獲利則為 144,000 元。

若要自己練習操作本範例，可以下載這個 Excel 範例檔案。

參考資料：Office 指南